Radians and Degrees in Rotational Position               

The position of objects moving in a straight line can be described in terms of one axis; say in the x direction. This is called one dimensional 1D- since it only take one number to describe the objects position. An example of this would be a train moving along a straight track. The position of an ant on the ground being viewed from above would be more complex. It may move in the x direction, or the y direction. Though is always on the ground- therefore in the same xy plane. This movement is called 2 dimensional 2D, since it requires two numbers to describe the ant's position.

A train is limited to the tracks- it cannot move sideways so its movement is along one dimension. It only takes one number to define its position. This is called one dimensional motion 1D	As viewed from above, an ant walking around on flat ground may move in two directions, in the x direction or the y direction. It takes two numbers to define its position. This is called two dimensional motion 2D.
The rotating disk, shown opposite shows points moving position in a rotating fashion in a plane. It is still 2 dimensional movement because all positions are still in the one plane, Rather than describing a position in terms of x and y, it is easier to describe rotational motion in terms of an angle it has rotated, and the distance it is from the axis of rotation r.

 

The angle can be measured in terms of degrees where 360 degrees would equal one rotation. It can also be measured in terms of the length of a radius of the circle placed around the path, making an arc. Since the circumference of a circle has length 2 radius, one rotation =2 radians.

1 circumference around the rotation = 360^o = 2 radians.
Therefore 1 radian = 360/(2) = 57.3^o.

Converting radians and degrees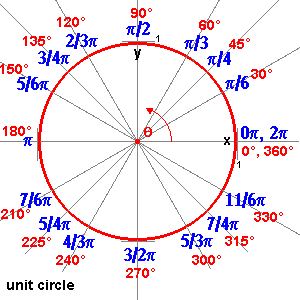

Convert 1 radian to degrees
Convert 90 degrees to radians
How many degrees are there in 2.5 radians?
How many radians are there in 530 degrees?